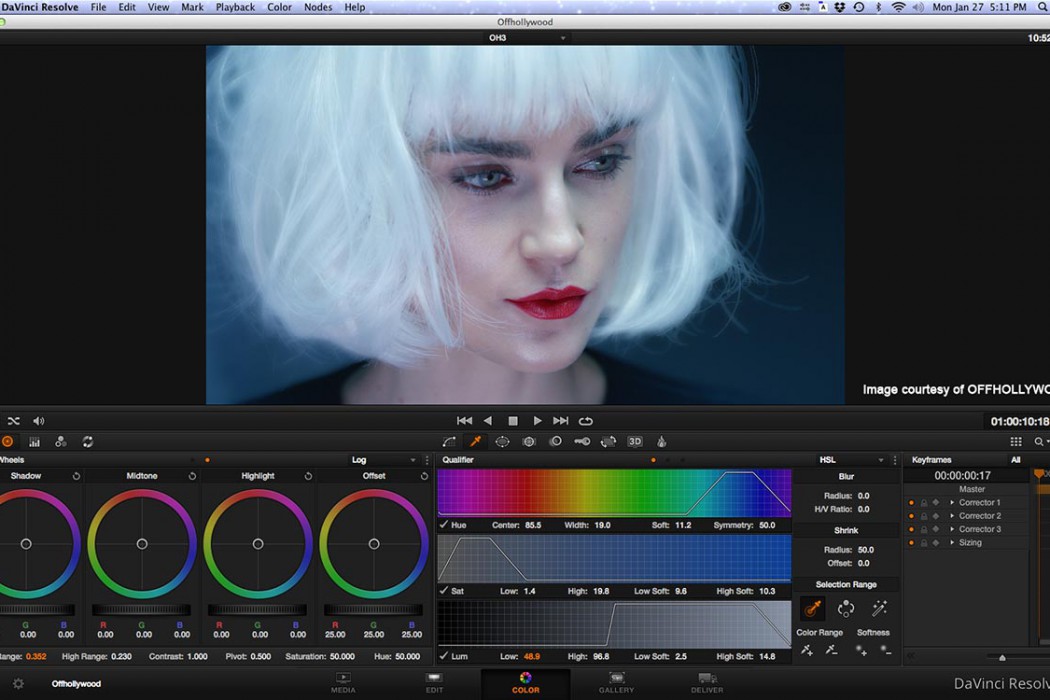
WHAT COLOUR IS THAT TEMPERATURE?
While most of us eventually absorb enough folk wisdom to deal with colour temperature, there are some aspects of it that simply aren’t intuitive.
Text:/ Andy Ciddor

Why does the colour of light get cooler as the colour temperature increases? If Lee 201 Full CT Blue converts 3200K tungsten light to 5700K daylight, why do two layers of 201 (or one layer of Lee 200 Double CT Blue) convert the same 3200K light to 26,000K? Is it actually possible to predict the outcome of combining correction filters?
Colour Temperature describes the colour (but not the brightness) of a light source by comparing it with the colours of light emitted by a standard object at a known temperature.
We are all familiar with what happens as you heat up a piece of metal. Initially the metal gets too hot to touch, but not hot enough to glow. Heat (infrared radiation) is being emitted, but as yet no visible light. Next, the metal starts to glow a deep red colour as it is now emitting visible light at the low energy end of the spectrum. As the temperature of the metal increases further, the energy of the emitted light also increases; progressively adding the higher energy wavelengths of the spectrum and changing the colour of the metal from orange, through yellow, to increasingly whiter light. However, in the world of real objects, as things get hotter, sooner or later they melt, oxidize, vaporize or catch fire. This makes it really hard to plot any simple curve relating a wide range of actual physical temperatures to light colours.
To solve this problem, a theoretical object named the Black Body Radiator was devised. It is a combination of the light emitting properties of a wide range of materials that can be heated until they glow. This object is black, so that it has no reflective properties.
Physicists have plotted the colours of light that would be emitted from this object at temperatures ranging from the theoretical Absolute Zero point (where all molecular activity ceases) to infinity. The temperature scale used for these measurements is Kelvin, which has absolute zero (-273.15ºC) as its starting point, and like the familiar Celsius scale, uses centigrade degrees as its steps. On the Kelvin scale, water freezes at 273.15 degrees (0ºC) and boils at 373.15 degrees (100ºC). The unit for measuring colour temperature is not the degree however, it’s simply the kelvin (K).
For example, the colour temperature of the DXX lamp in a Readhead is 3200 kelvin. This doesn’t mean the tungsten wire in the lamp is at a physical temperature of 3200ºK. What it actually means, is that the colour of the light coming from the Readhead’s lamp matches what would be emitted by the Black Body Radiator heated to a temperature of 3200ºK.

locus.
BUT IS IT ART?
Colour temperature terminology has nothing whatsoever do with the way that colour is described in the world of art. Whether or not you have any recollection of art lessons, you were almost certainly introduced to the notion of Newton’s colour wheel and complimentary colours at some point in your education. Frequently included with this view of colour comes the eighteenth century artists’ concept of warm and cool colours. In this framework, the low energy colours — reds, yellows and oranges — are considered Warm and Visually Active, while the higher energy blues and greens are classified as Cool and Visually Passive. Unfortunately, this view of colour is the total opposite of the relationship between colour and physical temperature in light sources.
As the temperature of an object rises during heating there are more high energy wavelengths (blues, greens, mauves and violets) in the light it emits, so the light looks whiter or ‘cooler’ in artistic terminology. In short: physically hotter equals artistically cooler. What could possibly be more straightforward?

THE KELVINATOR
Colour temperature corrections and conversions form an important part of the process of image production and image capture, in a wide range of AV applications. Once you venture outside the realm of matching the light from a tungsten halogen lamp at 3200K, and nominal daylight at 5500K/5700K, colour temperature correction starts getting a bit weird.
As you can see from the accompanying plot of the colour of light emitted by the Black Body Radiator during heating, the proportions of the colours emitted don’t follow a simple straight line. Consequently, a filter that removes specific colours for colour temperature matching, will have very different outcomes depending on the colour temperature of the originating light source. This is why the same CTB (Colour Temperature Blue) filter that converts 3200K light to 5700K, will convert a 5700K source all the way up to 26,000K, or a standard household lamp at 2000K up to only 2750K.
MIRED IN HISTORY
The worlds of photography and cinematography long ago hit on a useful, if not entirely straight forward, technique for handling colour temperature corrections by working with mireds (see below: ‘The Making of a Mired’). Using this method, every colour temperature is converted to its mired value and the correction factor of each filter is expressed as a mired shift with a positive or negative sign to indicate the direction of the shift. The mired shift is listed in the manufacturers’ swatch books and on their websites. A negative shift value indicates that the filter increases colour temperature (it’s a blue filter), while a positive mired shift indicates that the filter lowers colour temperature (it’s an orange filter).
It’s important to be aware that mired shifts differ between brands of what may appear to be equivalent correction filters. Rosco Cinegel CTB (#3202) has a mired shift of –131, while Lee 201 CTB has a shift of –137. Cinegel Roscosun CTO (#3407) has a mired shift of +167, while Cinegel Roscosun 85 (#3401 — often also referred to as CTO) has a mired shift of +131. And just to be completely different, the CTO in the Lee range (204) has a mired shift of +159.
Equipped with a simple calculating device and a filter swatch book, we can now take a starting colour temperature and a desired destination colour temperature, and with a little basic arithmetic, we can calculate which filters will give us the desired correction.
Let’s consider an everyday application of this process.
TEMPERATURE PRACTICALITIES
If we need to capture the image of a presenter at a lectern pointing to details on a nearby plasma or LCD display screen, we not only need to match light levels between the presenter and the screen, we also need to match colour temperatures. This will avoid the common problem of the screen looking blue or the presenter looking orange. Then we can correctly expose and white balance the camera capturing the image.
If there are a couple of profile spots (or theatrical fresnels) covering the lectern, they will need to be converted from their native 3000K up to the (approximately) 6500K of the plasma/LCD screen.
The plasma/LCD screen will generally be colour adjustable somewhere in the range of about 6500K (the SMPTE standard for television displays) to 9500K. The higher colour temperature settings are there because viewers seem to prefer cooler, bluer whites, even if they attain them at the expense of accurate colour representation.
To achieve our colour match we have a starting point of 3000K or 333 mired and a desired destination of 6500K or 154 mired. To make this conversion we need to apply a correction of approximately –179 mired (333 minus 154) in the blue or minus direction.
No single filter will do the job, but a combination of Lee 201 CTB (–137 mired) and Lee 203 ¼ CTB (–35 mired) will be sufficiently close (–172 mired), with a resulting colour temperature of approximately 6200K.
The camera will need to be configured for use in daylight, then white balanced on a reference card or alignment chart illuminated by the corrected 6200K light sources.
DIY — THE EASY WAY
To simplify the mired calculation process there is a mired calculator we’ve made available below. It calculates colour temperatures and colour temperature differences in mireds. It also calculates the colour temperature resulting from placing correction filters over a given light source.
There is a calculator with similar capabilities on the Lee website (link below) that goes as far as suggesting which filters from the Lee range will give the required correction. Be warned that some of the results it returns include the use of correction filters for other types of light sources which are totally unsuited to our application.
Colour correction for light sources that don’t match the curve of the Black Body Radiator, such as LEDs, fluorescents, arcs, and metal halide discharge (including HMI, MSR, CID), is a can of worms that will be opened in a future AV article. However, for the moment it remains a world of pain and confusion that we will avoid.

THE MAKING OF A MIRED
The relationship between the temperature of the Black Body Radiator and the proportions of the colours of light it emits, turns out to be a reciprocal function. Thus, by working with the reciprocals of colour temperatures, we get a reasonably simple method for calculating the effects of colour correction filters on light sources.
As revision for those who were traumatised for life by fractions at primary school: the reciprocal of any number is one divided by that number or ¹/n. The reciprocal of 2 is ½ or 0.5, and the reciprocal of 500 is ¹/500 or 0.002. As the reciprocals of large numbers are small numbers, using the reciprocals of colour temperatures produces fiddly results with several zeroes after the decimal point. For example, the reciprocal of the 3200K from our tungsten halogen lamps is 0.0003125, hardly a number that lends itself to memorisation or a quick calculation on your phone. Hence the choice to use mireds or micro-reciprocal degrees (one million divided by the colour temperature) for photographic applications.
After rounding, tungsten light’s 3200K is a manageable 313 mireds. Some physicists with nothing better to do than annoy a lot of already confused people, have suggested that we drop the name mireds in favour of the SI standards-compliant term ‘reciprocal megakelvins’ (MK-1). Thus far the suggestion has been ignored by the industry.














RESPONSES